Lecture 11

Andreas Moshovos

Fall 2007

Revised 2024

A complete function example: The Ackerman recursive subroutine.

The following C code computes the Ackerman function:

int

Ackerman(unsigned int x, unsigned int y)

{

if (x == 0) return y+1;

if (y == 0) return Ackerman (x-1, 1);

return Ackerman (x-1, Ackerman(x, y-1));

}

This is an interesting to implement function because it’s recursive and also shows how to use a function call as an argument to call another function.

An equivalent implementation of Ackerman that illustrates what is supposed to happen in the last line is as follows:

int

Ackerman(unsigned int x, unsigned int y)

{

int tmp;

if (x == 0) return y+1;

if (y == 0) return Ackerman (x-1, 1);

tmp = Ackerman(x, y-1);

return Ackerman (x-1, tmp);

}

Let’s first figure out what needs to be saved on the stack. We definitely need to save the return address since Ackerman calls functions. We also need to preserve the value of parameter x across the call to function Ackerman(x, y-1). We do not need to preserve y since we never needed after a call. So, in total we need space for two words. Here’s what the stack frame will look like after Ackerman’s prologue:

sp à	+0	Saved r4 / argument x
	+4	Saved ra / return address

Here’s an implementation in NIOS II assembly:

.text

Ackerman:

# Prologue

addi sp, sp, -8

stw ra, 4(sp)

# if (x == 0) return y +1

# we write this as:

# if (x != 0) skip over the code that returns y + 1

bne r4, r0, Xnot0

Xis0:

# return value is y + 1

addi r2, r5, 1

# done, return from the function

br epilogue

Xnot0:

# test if y is 0 and return Ackerman (x – 1, 1)

bne r5, r0, Ynot0

Yis0:

# pre-call

# pass arguments

# first argument is x-1

addi r4, r4, -1

# second is 1

addi r5, r0, 1

call Ackerman

# the return value is already in r2, exit the function

br epilogue

Ynot0:

# first call Ackerman (x, y-1)

# pre-call

# preserve the value of x on the stack

stw r4, 0(sp)

# pass arguments

# x is in the right place

# decrement y by 1

addi r5, r5, -1

call Ackerman

# post-call

# restore x

ldw r4, 0(sp)

# call Ackerman (x-1, tmp) where tmp is the value returned from Ackerman (x, y-1)

# pre-call

# decrement x by 1 and pass as first argument

addi r4, r4, -1

add r5, r2, r0

call Ackerman

# return value is already in r2

epilogue:

# Epilogue

# restore ra and de-allocate stack space

ldw ra, 4(sp)
addi sp, sp, 8

ret # return to caller

A closer look at how we can figure out what needs to be preserved across calls

Let us now look at a more systematic way of determining what register values need to be preserved across a call site.

Control Flow: The figure below shows the control flow graph of the function:

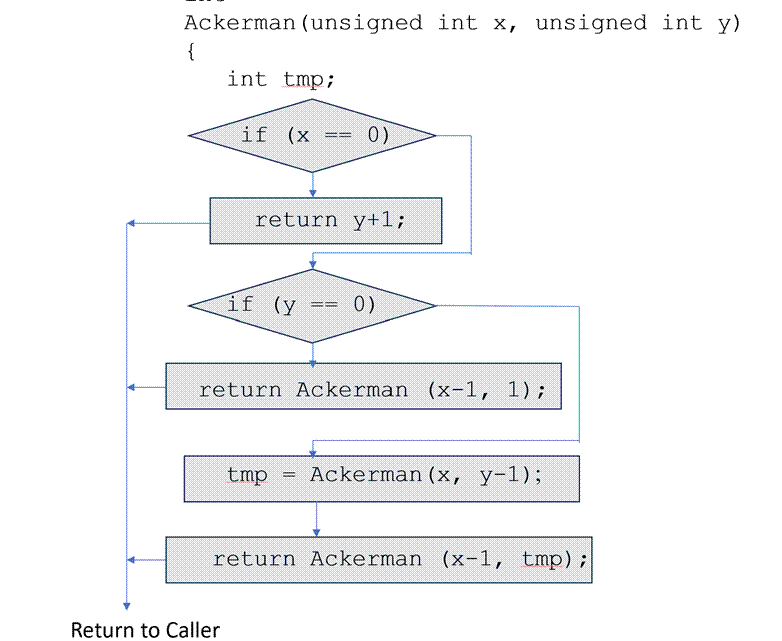
Paths through the Control Flow Graph: There are three partially overlapping execution paths through the code. All three (1), (2), and (3), pass through the first if condition (x == 0). Path (1) exits if the condition is true returning y+1. Paths (2) and (3) continue and evaluate the second if condition (y == 0). They diverge depending on whether the condition is true (path (2)) or false (path (3)). Path (2) calls Ackerman (x-1) while path (3) performs two calls to ackerman before returning.

Lifetime Analysis: The function accepts as input x and y. Let us now consider all three possible paths trying to determine whether x and y remain “live” at each point along the path. We care about x and y because when the function is called, they are in r4 and r5. By convention those two registers are caller saved. That is, if we care for their values and we do a call, we have to preserve them by saving and restoring them across the call (this is done typically by pushing them on the stack).

A value is live at some block along a path, if we expect that we will use it in some other block that we might encounter later on in the path. This is best understood by walking through our example. Let us first annotate where the input values are used. Ultimately, what we are interested in are values that need to survive across a call to a function. Those are values that need to be explicitly preserved and need to reside either a callee saved register or on the stack. We are looking for scenarios where:

Rx has a value and is in a caller saved register

Call some_function

Use Rx expecting that it still holds the same value it did before the call.

This will become clearer as we go through the example.

Let’s first consider path (1):

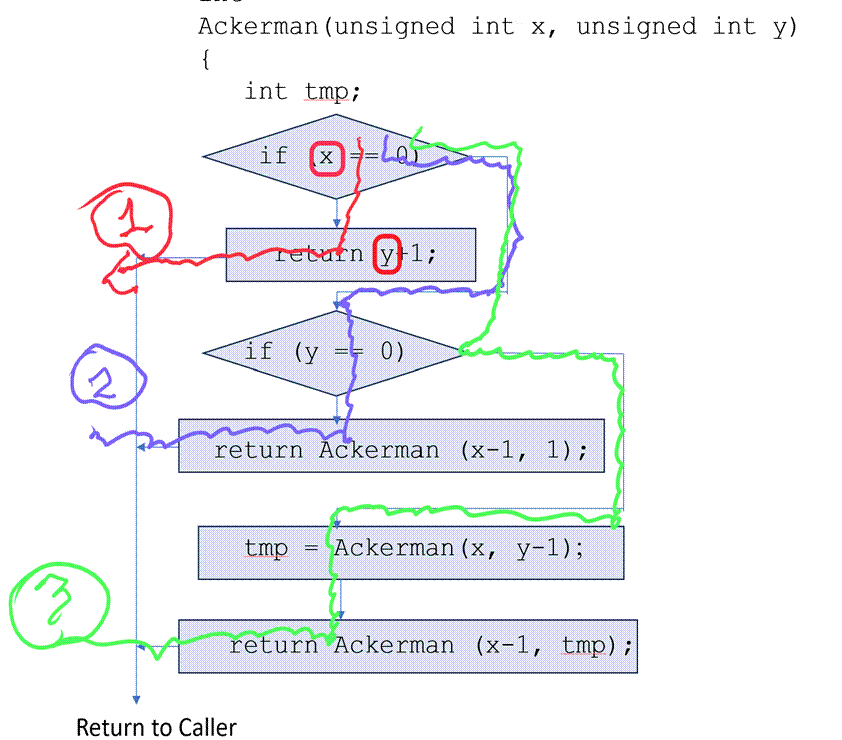
There are two uses of x and y in this path as noted by the colored boxes. There are no calls before any of the two uses of x and y. So, we do not need to save and restore them across a call since there is no call :)

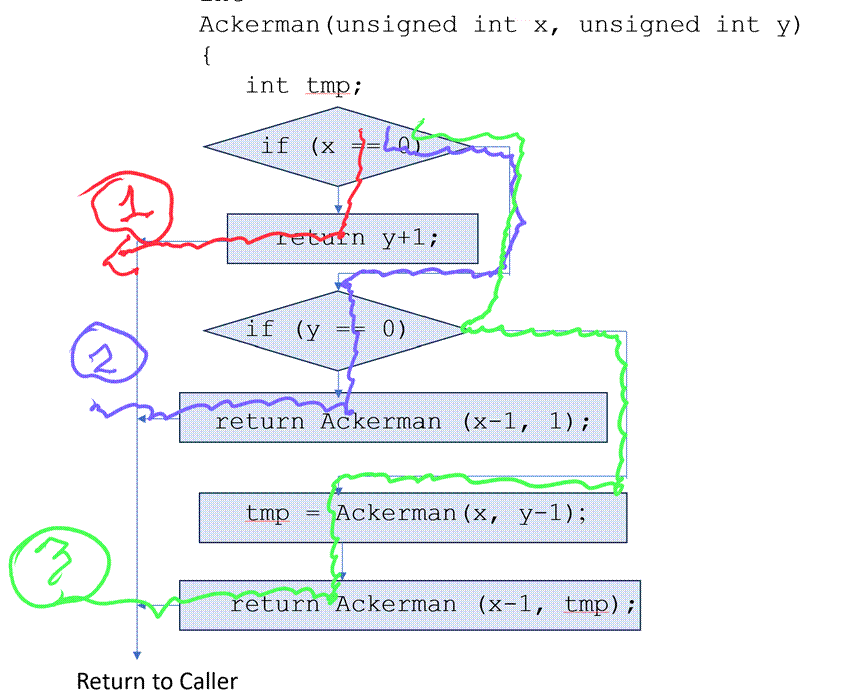
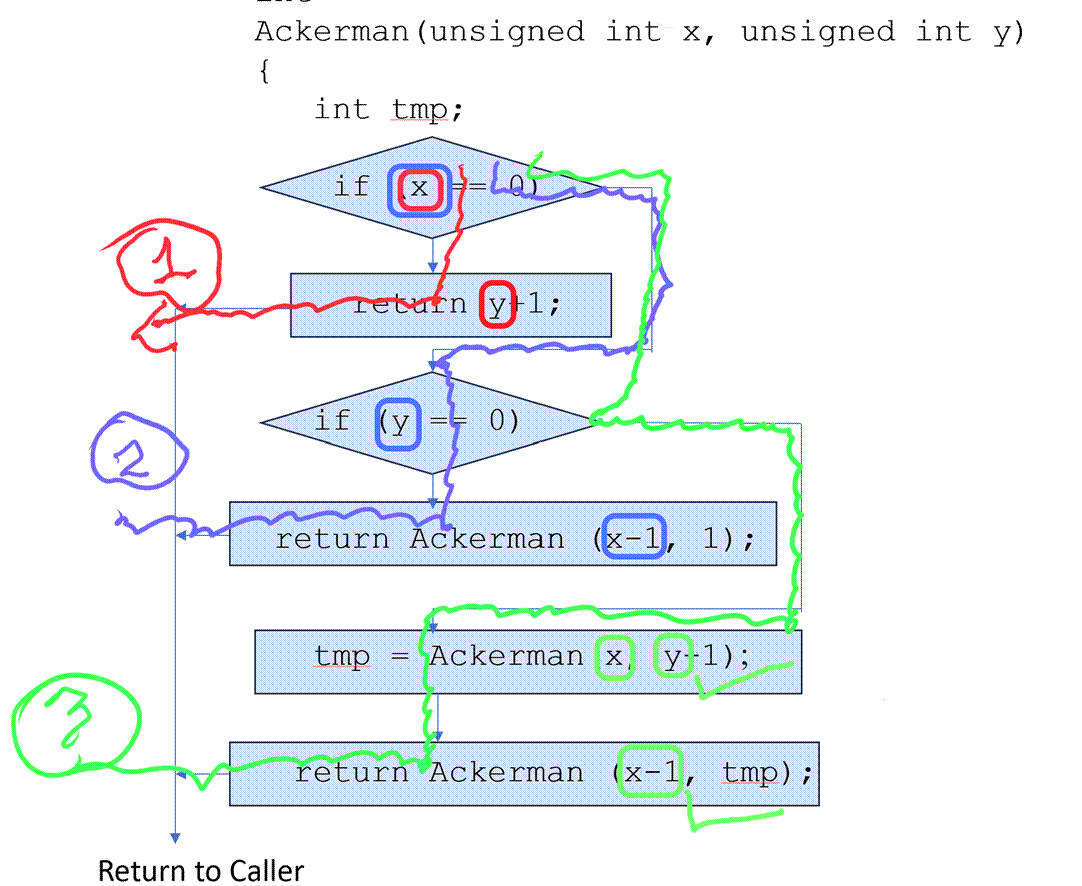
Now let’s look at path (2). In the following diagram we annotated those using blue boxes:

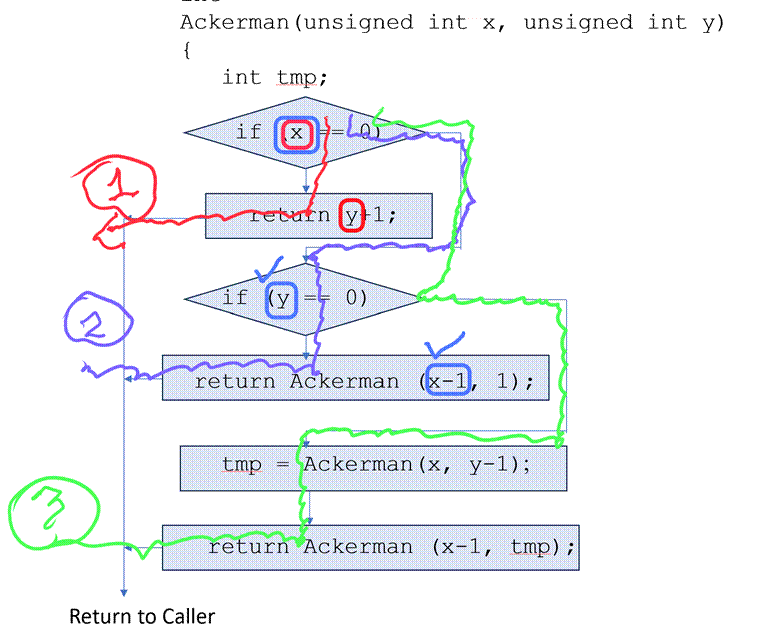
We also added checkmarks next to the last use of x and y. As in path (1) none of the uses are *after* a call. The last use of x is where it is being used as an argument to Ackerman(x-1,1). This means that before we call Ackerman there, we will need to take the existing x in r4 and substract 1 from iti. Then it becomes the first argument to the call. After the call, we return, thus we no longer care for the original x. For y, things are simpler. We use it only for evaluating the second if condition and from that point on, in path (2) we no longer care for it.

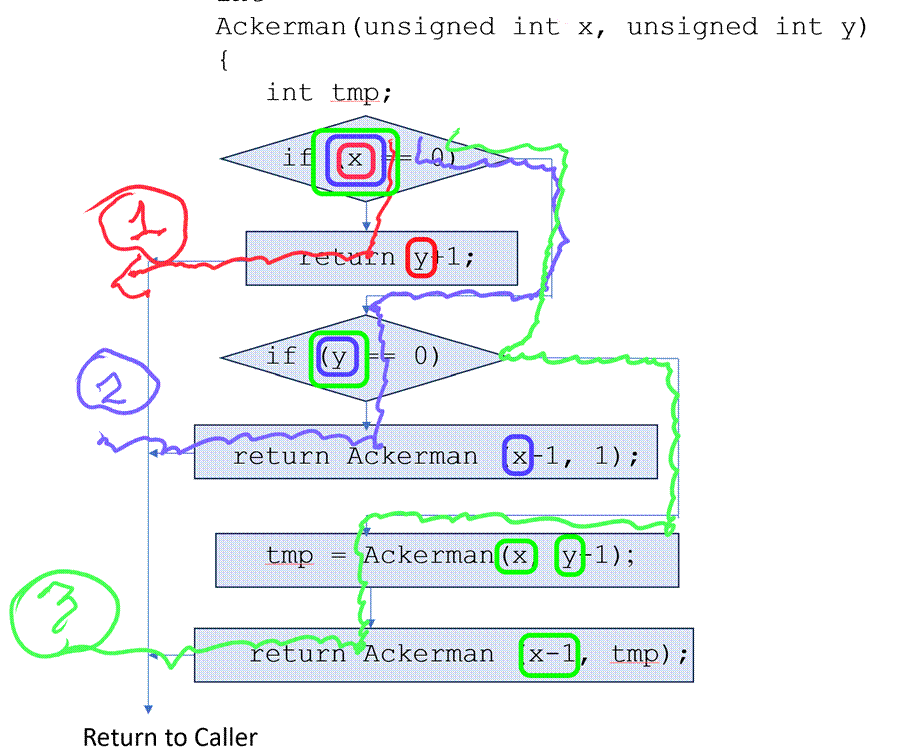
Finally, let’s look at path (3) (uses of x and y are now annotated with green boxes and the last use of each is marked with a check mark):

The last use of y is just before the first call to Ackerman (tmp = Ackerman(x, y-1)). After that we no longer care about y. However, look at x. The last use of x is in the second call to Ackerman. This means that x needs to “survive” the first call. So, x is live across the first call to Ackerman along path (3) and for this reason it needs to be preserved since we will be making a call, and presently it is held in r4 which is a caller-saved register. This is why we make space on the stack and we save it there.

If you want to dive a bit deeper than this, consider what other options might existed for preserving r4. One option might have been to copy the value in a callee-saved register and to do so just before the call. Something like this:

Mov r16, r4

Call Ackerman

// r16 still holds the value it had before the call since it is a callee-saved register

However, since r16 is a callee-saved register and since we are function as well we cannot simply use it anytime we wish. Whoever called us, expects that any value they left there, if any (we don’t know whether they care), will remain intact. So, before we overwrite the existing value in r16 we need to save its existing value on the stack. At the end, we are still saving and restoring a value from the stack either way. What further limits our options here is that Ackerman calls itself.