For loops and arrays – more examples

Andreas Moshovos, Jan 2024, Fall 2024

Let’s look at another example of a for loop going over an array:

#define N 10 // elements in the array

#define T 5 // T stands for threshold

int a[N] = { some values };

int sum = 0;

int i;

for (i = 0; i < N; i++)

if (a[i] >= T) sum += a[i];

The above code adds up all elements in a[i] whose value exceeds or is equal to some threshold value T.

The control flow diagram for the code is as follows:

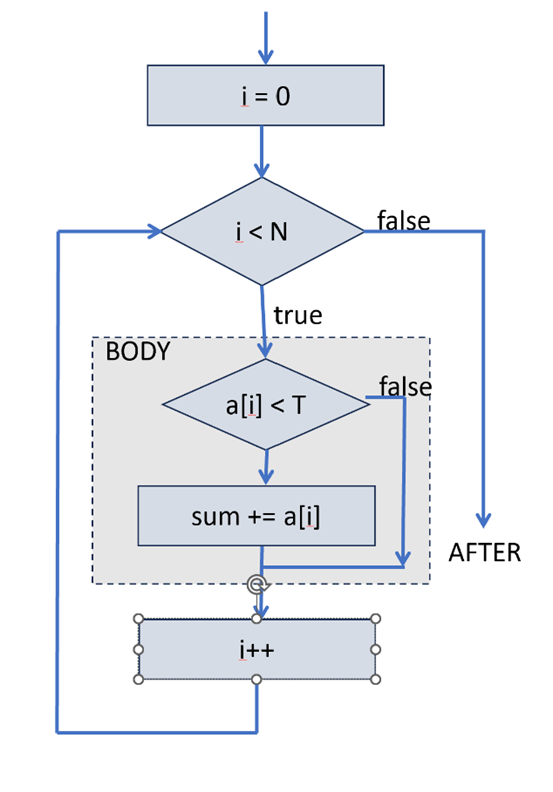
As programmers we have to decide where to place the variables. Since a[] is an array it will be placed in memory. We can declare it with a statement that looks as follows:

.data

a: .word list_of_values_goes_here

In the rest of this note we will assume that a[] has been declared and initialized and we will refer to the label “a”. As we discussed, “a” from this point on becomes the address in memory where a[0] will be stored at. For example, a[0] could be 0x200000. Since every element is a word (4B), then a[1] will be at 0x200004, a[2] at 0x200008, and so on. In general, a[i] will be stored as 4B starting at address (a + 4 x i).

Let’s now decide that i will be stored in r2 and sum in r8.

The code is as follows:

A0 r8 a1 r2 a2 r4 a3 r5 a4 r6 a5 r7 a6

example:

li a0, 0 # sum = 0

li a1, 0 # i = 0, INIT of loop

cond:

li a2, 10 # a2 = N

bge a1, a2, after # if i >= N we are done

body:

# a[i] < T

li a3, 5 # a3 = T

# let’s find where a[i] is at

la a4, a

add a5, a1, a1 # a5 = 2xi

add a5, a5, a5 # a5 = 4xi

add r6, a4, a5 # a4 = a + 4 x i / address where a[i] is at

lw a5, 0(a4) # a5 = a[i] / read a[i] from memory

bge a5, a3, post # if a[i] >= T do not add to sum

addsum:

add a0, a0, a5 # sum += a[i]

post:

addi a1, a1, 1

breq x0, x0, cond

That’s all. Now, can we find any instructions that execute in the loop but whose output register does not change in value across iterations? Loop at the l1 a2, 10 in the cond block. It always assigns 10 to a2 and it does so once per iteration. What if we move this instruction just before the loop? Will the final values calculated by the loop change? This is what we’ve done below:

example:

li a0, 0 # sum = 0

li a1, 0 # i = 0, INIT of loop

li a2, 10 # a2 = N – moved to INIT code block

cond:

bge a1, a2, after # if i >= N we are done

body:

# a[i] < T

li a3, 5 # a3 = T

# let’s find where a[i] is at

la a4, a

add a5, a1, a1 # a5 = 2xi

add a5, a5, a5 # a5 = 4xi

add r6, a4, a5 # a4 = a + 4 x i / address where a[i] is at

lw a5, 0(a4) # a5 = a[i] / read a[i] from memory

bge a5, a3, post # if a[i] >= T do not add to sum

addsum:

add a0, a0, a5 # sum += a[i]

post:

addi a1, a1, 1

breq x0, x0, cond

At the end, even with this change, the loop produces the same values. Why would we want to move such instructions out of the loop? Well, in the end, while the code produces the same results, it does so by executing fewer instructions. This means it is faster and uses less energy. Usually both these are advantages. Such instructions and code are referred to as “loop invariant” meaning they do not change across loops.

Can you spot other such instructions? HINT: this is not a wild goose chase. There are more.

Revisiting how we access the array

Let’s us revisit the C code we wrote for summing some of the elements of the array:

int i;

for (i = 0; i < N; i++)

if (a[i] >= T) sum += a[i];

We can note that in this loop we know that i will increment by 1 at every iteration. However, the way the code is written we have to calculate where in memory a[i] is from scratch as every iteration. We do not take advantage of the fact that we are going over all array elements one after the other in sequence. We know that next(i)=current(i)+1. Given this observation, we can instead write the loop as follows where we use a pointer in memory (p) to walk through the elements of the array:

int i;

int *p;

p = &a[0];

for (i = 0; i < N; i++, p++)

if (*p >= T) sum += *p;

The pointer p is just a 32b value which we intend to use as an address to access memory (load values in this case). It is 32b because in NIOS II the memory address space is 2^32 and all addresses are 32b. In other architectures pointers can be of different bit length.

The statement *p = &a[0] can also be written as p = a. In both cases, we assign into variable p, the address of the first element of array a.

Let’s see what the above code translates to. Below we assume that sum is in a0, i in a1, and p in a2:

la a2, a # p = a

li a0, 0 # sum = 0

li a1 0 # i = 0

li a3, 10 # a3 = N

li a4, 5 # a4 = 5 = T

cond:

bge a1, a3, after

body:

lw a5, 0(a2) # r13 = *p // we are reading a[i] into r13

blt a5, a4, post # a[i] < T then skip the sum

usum:

add a0, a0, a5 # sum += r13

post:

addi a1, a1, 1 # i++

addi a2, a2, 4 # p++, p points to int so we increment by the sizeof(int) = 4

beq x0, x0, cond

In the above code, we use p to access the elements of a[] one after the other. P points to the next element to process. We start with p pointing to a[0], and at every iteration we increment it by 4 so that we access the next element in order.

We can further optimize the code by getting rid the i variable and use p and the size of the array to check whether we processed all elements:

int i;

int *p, *p_last;

p = &a[0];

p_last = p + N; // address immediately after the last element of a[] since there are N elements in it

for (; p < p_last; p++)

if (*p >= T) sum += *p;

and in assembly:

la a2, a # p = a

li a0, 0 # sum = 0

addi a1, a2, 40 # p_last = a + 10 elements x 4B per element

li a4, 5 # a4 = 5

cond:

bge a2, a1, after

body:

lw a5, 0(a2) # r13 = *p // we are reading a[i] into r13

blt a5, a4, post # a[i] < T then skip the sum

usum:

add a0, a0, a5 # sum += r13

post:

addi a1, a1, 1 # i++

addi a2, a2, 4 # p++, p points to int so we increment by the sizeof(int) = 4

beq x0, x0, cond