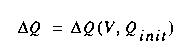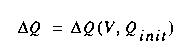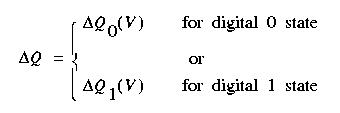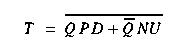ZSTT: A Ferroelectric Capacitor Macromodel

ZSTT: A Ferroelectric Capacitor Macromodel:

This page provides detailed description of a ferroelectric capacitor macromodel, called Zero Switching Time Transient (ZSTT) Model.

Zero Switching-Time Transient (ZSTT) Model:

As its name suggests, the ZSTT model assumes the switching time of a ferroelectric capacitor to be zero. This assumption will introduce little inaccuracy if the RC time constant of the circuit under study is much larger than the switching time of the FE capacitor. It is shown [1] that for a typical memory circuit including FE capacitors such an assumption is quite valid.

Zero switching-time implies that a charge increment on the FE capacitor will take place instantaneously. Therefore, a charge increment is only a function of the applied voltage and the initial state of the capacitor, not a function of time. In other words:

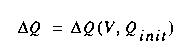where V and Qinit represent the applied voltage and the initial polarization charge on the capacitor. Since there are only two initial states that are important to a memory cell (i.e. digital 0 and 1), the above equation can be broken into two parts, each corresponding to one initial state. In other words:

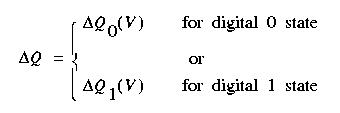This equation is further represented as a state diagram:

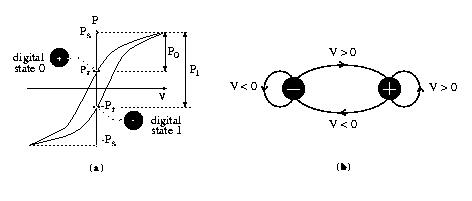A positive voltage pulse, for example, brings the capacitor to a digital 0 state if it is initially in a digital 1 state. This state transition corresponds to a charge increment of DQ1 followed by a charge decrement of DQ0 -both of them functions of the pulse amplitude. The pulse-measurement approach discussed in [1] approximates DQ0(V) and DQ1(V) with two piecewise-linear functions of voltage. Each piecewise-linear function is implemented as a piecewise-linear capacitor that exists in most circuit simulators.

model Implementation:

A circuit representation of the ZSTT Model is shown in in the following:

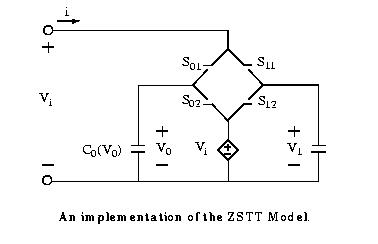C0(V0) and C1(V1) represent the two nonlinear capacitors corresponding to the two binary states of the FE capacitor discussed earlier. If the binary state of the FE capacitor is 0, switches S01 and S12 are closed while switches S11 and S02 are open. In this case, the equivalent capacitance looking into the input terminals is C0(V0). Meanwhile, a voltage controlled voltage source, which is equal to Vi , is connected to C1(V1) to initialize this capacitor for the opposite binary state. For binary state 1, the states of the switches are the reverse: switches S11 and S02 are closed while switches S01 and S12 are open. Therefore, the capacitance looking into the input terminals is C1(V1), and the controlled source is connected to C0(V0) for the similar reason mentioned above.

If the initial binary state of an FE capacitor is known, its subsequent binary states can be determined by the applied pulse pattern. A binary state 0 remains unchanged in response to a positive pulse as well as the leading edge (falling edge) of a negative pulse. It only changes on the trailing edge (rising edge) of the negative pulse. A binary state 1 remains unchanged in response to a negative pulse as well as the rising edge of a positive pulse. It only changes on the falling edge of the positive pulse.

The ZSTT Model can be easily implemented as an HSPICE macro-model if the two nonlinear capacitors in Fig. 10 are replaced by their piecewise linear approximations. The switches can be replaced by voltage- controlled resistors (VCRs) that exhibit high and low resistances for the open and closed states of the switches, respectively. The logic circuit shown:

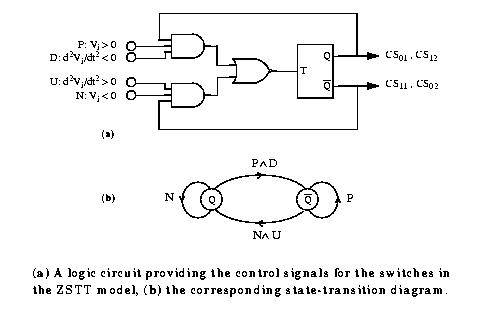provides appropriate control signals for the switches. The flip-flop toggles with the falling edge of T, where:

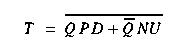The toggle flip-flop and the logic gates are all implemented in HSPICE.

One example of an input voltage pattern and its corresponding control signals for the switches are illustrated here:

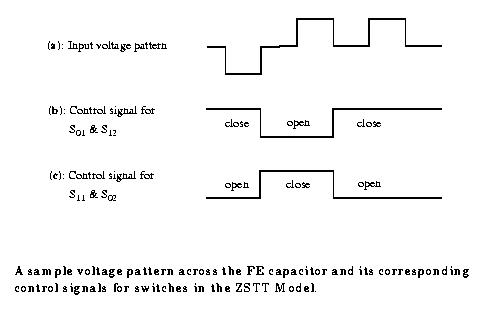The initial binary state of the capacitor, in this example, is considered to be 0. Therefore, S01 and S12 are initially closed (CS01 = CS12 = High), and the equivalent capacitance looking into the input terminals is C0(V0). On the rising edge of the first negative pulse, switches S11 and S02 are closed (CS11 = CS02 = logic 1) and switches S01 and S12 are opened (CS01 = CS12 = logic 0). In this case, the capacitance looking into the input terminals is C1(V1). This situation will be reversed again on the falling edge of the first positive pulse.

References:

[1] A. Sheikholeslami and P. Glenn Gulak, "Transient Modeling of Ferroelectric Capacitors for Nonvolatile Memories", IEEE Trans. on UFFC, Vol. 43, No. 3, pp. 450-456, May 1996

This work was supported by Nortel and the Natural Sciences and Engineering Research Council of Canada.